![]() §24.4(1)相似三角形的断定
§24.4(1)相似三角形的断定
1、已知一个三角形内角分别为![]() ,另一个三角形内角分别为
,另一个三角形内角分别为![]() ,则这两个三角形……
,则这两个三角形……
肯定相似 未必相似 肯定不相似 不可以确定
 2、如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有……
2、如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有……
1对 2对 ![]() 3对 4对
3对 4对
3、如图,△ABC中,DG、DF、EG分别平行于BC、AC、AB,图中与△ADG一样的三角形共有 __________个
4、如图,△ABC中,D在AB上,若∠ACD=∠B,AD=4,AB=6,则AC=__________
__________
5、如图,E是□ABCD的边BA延长线上的一点,CE交AD于点F,图中__________对相似三角形。

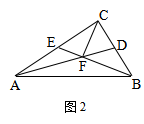
 __________
__________
图(1) 图(2) 图(3)
 6、如图,矩形ABCD中,BP⊥PQ,求证: △ABP∽△DPQ; 写出对应边成比率的式子.
6、如图,矩形ABCD中,BP⊥PQ,求证: △ABP∽△DPQ; 写出对应边成比率的式子.
 7、已知:在△ABC中,点D、E分别在AC、AB边上,且∠ADE=∠B,若AE=2,BE=3,AD=3,求CD的长。
7、已知:在△ABC中,点D、E分别在AC、AB边上,且∠ADE=∠B,若AE=2,BE=3,AD=3,求CD的长。
§24.4(2)相似三角形的断定
1、下列能断定△ABC和△DEF一样的是( )
(A)∠A=40°,∠B=∠E=58°,∠D=82°;(B)∠A=∠E,![]() ;
;
(C)∠A=∠B,∠D=∠E; (D)AB=BC=DE=EF.
2、如图,AD和BE分别是三角形的高,则图中相似三角形有( )
(A)4对; (B)5对; (C)6对; (D)7对.
3、如图,点P是△ABC边AB上一点(AB>AC),下列条件未必能
使△ACP∽△ABC的是( )
(A)![]()
![]() ; (B)
; (B)![]()
![]() ;
;
(C)∠ACP=∠B; (D)∠APC=∠ACB.
4、下列说法中,正确的是( )
①有两边成比率且一对内角相等的两个三角形相似;②有一对锐角相等
的两个直角三角形相似;③有两边对应成比率且夹角相等的两个三角形
相似;④一条直线截三角形两边所得的三角形与原三角形相似.
(A)①,②;(B)②,③;(C)③,④;(D)①,④.
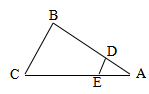
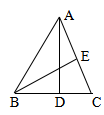
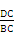
![]()
第2题图 第3题图 第5题图
5、如图,在△ABC中,DE∥BC,![]()
![]() ,则△ABC∽__________,其相似比为__________.
,则△ABC∽__________,其相似比为__________.
![]()
 6、如图,一张长8cm,宽6cm的矩形纸片,将它沿某直线折叠使得A、C重合,求折痕EF的长.
6、如图,一张长8cm,宽6cm的矩形纸片,将它沿某直线折叠使得A、C重合,求折痕EF的长.
 7、如图,∠C=90°,AC=CD=DE=BE,试找出图中的一对相似三角形,并加以证明.
7、如图,∠C=90°,AC=CD=DE=BE,试找出图中的一对相似三角形,并加以证明.
§24.4 (3)相似三角形的断定
1、在△ABC中,直线DE分别与AB、AC相交于点D、E,下列条件不可以推出△ABC与△ADE一样的是( )
(A)![]()
![]() ; (B)∠ADE=∠ACB;
; (B)∠ADE=∠ACB;
(C)AE﹒AC=AB﹒AD; (D)![]()
![]() .
.
2、已知△ABC和△ADC均为直角三角形,点B、D坐落于AC的两侧,
∠ACB=∠ACD=90°,BC=a,AC=b,AB=c,要使△ADC和△ABC相似,
CD可以等于( )
(A)![]()
![]() ; (B)
; (B)![]()
![]() ; (C)
; (C)![]() ; (D)
; (D)![]()
![]() .
.
3、下列各组图形大概不一样的是( )
(A)各有一个角是45°的两个等腰三角形;
(B)各有一个角是60°的两个等腰三角形;
(C)各有一个角是105°的两个等腰三角形;
(D)两个等腰直角三角形.
4、点D在△ABC的边AB上,且AC2=AD﹒AB,则△ABC∽△ACD,理由是____________________.
5、如图,在△ABC中,点D、E分别在边AB、AC上,已知AB=6,AC=9,BC=
 12,AD=3,AE=2,那样DE=__________.
12,AD=3,AE=2,那样DE=__________.
6、在△ABC中,D为AB上一点,且AD=1,AB=4,AC=7,若AC上有一点E,且△ADE与原三角形相似,则AE=__________.
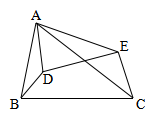 7、如图,D为△ABC内一点,E为△ABC外一点,且满足
7、如图,D为△ABC内一点,E为△ABC外一点,且满足![]()
![]() ,
,
求证:△ABD∽△ACE.
§24.4 (4)相似三角形的断定
1、RT△ABC,∠ACB=90°,CD⊥AB于点D,下列等式成立的是( )
(A)AD2=AB﹒AC; (B)AC2=AB﹒AD;
(C)AB﹒AC=BD﹒DC; (D)AB﹒CD=BD﹒AC.
2、在RT△ABC和RT△DEF中,∠C=∠F=90°,由下列条件断定△ABC
∽△DEF的是( )
①∠A=55°,∠D=35°;②AC=3,BC=4,DF=6,DE=8;③AC=9,BC=12,
DF=6,EF=8;④AB=10,AC=8,EF=9,DE=15.
(A)1个; (B)2个; (C)3个; (D)4个.
3、点P是RT△ABC的斜边BC上异于B、C的点,过点P作直线截△ABC,使截得的三角形与原三角形相似,满足如此的直线共有__________条.
4、如图1,在直角梯形ABCD中,DC∥AB,DA⊥DC,DC=6,AD=8,
AC⊥BC,则AB=__________.
5、如图2,在矩形ABCD中,AB=2,CB=1,E是DC上一点,∠DAE=
 ∠BAC,则EC的长为__________.
∠BAC,则EC的长为__________.

6、如图,AB⊥AD,BD⊥DC,且BD2=AB﹒BC.求证:∠ABD=∠DBC.
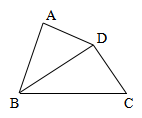
7、如图,在正方形ABCD中,E是CD上的一点,F是BC的延长线上的一点,且CE=CF,BE的延长线交DF于点G,求证:△BGF∽△DCF.
§24.4 (5)相似三角形的断定
1、将一张矩形纸片对折后裁下,得到两张大小完全一样的矩形纸片,已知它们都与原来的矩形相似,那样原来矩形长与宽的比为( )
(A)2:1; (B)![]()
![]() :
:
1; (C)3:1; (D)![]()
![]() :
:
1.
2、下列命题中,假命题是( )
(A)正方形都相似; (B)对角线和一边对应成比率的矩形相似;
(C)等腰直角三角形都相似; (D)底角为60°的两个等腰梯形相似.
3、在△ABC中,D为AB上一点,过点D作一条直线截△ABC,使截得
的三角形与△ABC相似,如此的直线可以作( )
(A)2条; (B)3条; (C)4条; (D)5条.
4、如图1,在△ABC中,DE∥BC,则![]()
![]() =__________.
=__________.
5、如图2,在RT△ABC中,∠ACB=90°,BA=12cm,AD、BE是两条中线,F为其交点,那样CF=__________cm.
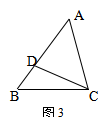
6、如图3,D为AB上一点,且AD=2BD,∠ACD=∠B,那样![]()
![]() =__________.
=__________.


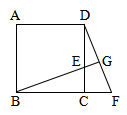
7、如图,在四边形ABCD中,∠B=∠D=90°,过点D作对角线AC的垂线,交AC于点E,交BC于点F,求证:CD是CF和CB的比率中项.
8、 如图,DF为RT△ABC斜边AB的中垂线,交BC及AC的延长线于点E、F,已知CD=6,DE=4,求DF的长.
§24.4(1)相似三角形的断定
1.答案:A
分析:两个内角对应相等的两个三角形相似
2.答案:C
分析:△ADE∽△ACD∽△ABC
3.答案:5
分析:图中所有其他的三角形都与△ADG相似
4.答案:![]()
分析:AC2=AD×AB=24,AC=![]()
__________
5.答案:3
分析:△AEF∽△FCD∽△EBC
6.答案:(1)证明过程如分析
(2)![]()
分析:(1)∵矩形ABCD,BP⊥PQ
∴∠A=∠D=∠BPQ=90°
∴∠ABP+∠APB =90°,∠DPQ+∠APB =90
∴∠ABP=∠DPQ
∴△ABP∽△DPQ
(2)![]()
7.答案:CD的长为![]()
分析:∵∠ADE=∠B,∠A=∠A
∴△ADE∽△ABC
∴![]()
∴![]()
∴AC= ![]()
∴CD= ![]()
§24.4(2)相似三角形的断定
1.答案:A
分析:两个内角对应相等的两个三角形相似
2.答案:C
分析:△AOE∽△BOD∽△ACD∽△BCE
3.答案:B
分析:有两边对应成比率且夹角相等的两个三角形相似,而B不是夹角相等
4.答案:B
分析:①需要是夹角,④需要是第三边的平行线
5.答案:△ADE;![]()
分析:∵![]() ,∴
,∴![]()
6.答案:EF的长为![]()
分析:联结CF
∵翻折
∴AF=CF
设AF=x,则DF=8-x
![]()
![]()
∵OC=5
∴OF=![]()
可证OE=OF
∴EF=![]()
7.答案:△ADE∽△BDA
分析:∵∠C=90°,AC=CD=DE=BE
∴AD=![]() ,BD=2
,BD=2![]()
∴![]()
∵∠ADB=∠ADB
∴△ADE∽△BDA
§24.4 (3)相似三角形的断定
1.答案:D
分析:有两边对应成比率且夹角相等的两个三角形相似,而D不是夹角相等
2.答案:B
分析:![]()
3.答案:A
分析:45°大概是顶角,也大概是底角
4.答案:有两边对应成比率且夹角相等的两个三角形相似
分析:![]() 且∠A=∠A
且∠A=∠A
5.答案:DE=4
分析:∵![]()
![]() ,∠A=∠A
,∠A=∠A
∴△ADE∽△ACB
∴![]()
∴DE=4
6.答案:![]() 或
或![]()
分析:分类讨论i.![]() ,
,![]()
ii .![]() ,
,![]()
7.答案:证明过程如分析
分析:∵![]()
∴△ADE∽△ABC
∴∠DAE=∠BAC
∴∠DAB=∠EAC
∵![]()
∴△ABD∽△ACE
§24.4 (4)相似三角形的断定
1.答案:B
分析:射影定理
2.答案:C
分析:①③④是正确的,②没边对应成比率
3.答案:4
分析:A字型或斜交型各2个
4.答案:![]()
分析:![]() ,
,![]() ,
,![]()
5.答案:![]()
分析:![]() ,
,![]() ,
,![]() ,
,![]()
6.答案:证明如分析
分析:∵AB⊥AD,BD⊥DC
∴△ABD和△DBC都是Rt△
∵BD2=AB﹒BC
∴![]()
∴Rt△ABD∽Rt△DBC
∴∠ABD=∠DBC
7.答案:证明如分析
分析:∵正方形ABCD
∴∠DCB=∠DCF=90°,DC=BC
∵CE=CF
∴△DCF≌△ECB
∴∠CDF =∠CBE
∵∠CDF+∠F=90°
∴∠CBE+∠F=90°
∴∠BGF=90°=∠DCF
∴△BGF∽△DCF
§24.4 (5)相似三角形的断定
1.答案:B
分析:设矩形长2a,宽b,则![]() ,
,![]() ,
,![]()
2.答案:B
分析:B没说了解一边是矩形的长还是宽
3.答案:C
分析:A字型或斜交型各2个
4.答案:![]()
分析:三角形一边的平行线性质定理推论
5.答案:4
分析:AB上的中线长为6cm,由于点F是重心,所以CF长为![]() cm
cm
6.答案:![]()
分析:∵∠ACD=∠B,∠A=∠A
∴△ACD∽△ACB
∴![]()
∴![]()
![]()
![]()
![]()
∴![]()
![]()
7.答案:证明如分析
分析:∵∠ACD= ∠ACD,∠DEC=∠CDA
∴△DEC∽△CDA
∴![]()
同理可得△FEC∽△CBA
∴![]()
∴![]()
∴![]()
∴CD是CF和CB的比率中项
8.答案:9
分析:∵DF为RT△ABC斜边AB的中垂线
∴∠BDE =90°,![]()
∵DE=4
∴![]()
∵∠ACB= ∠BDE,∠B=∠B
∴△ACB∽△BDE
∴![]()
∴![]()
∴![]()
同理可得△ADF∽△CBA
∴![]()
∴DF=9







